12th February 2015

By Dr Simon Kirby, Mathematics Department

One of the things that I really love about maths is being able to find out something new by arguing about things that I know, can see, can discuss or can link together.

For instance, a common method for dividing by a fraction is "take the second fraction, flip-it, and then multiply".

Great. ...why?

As soon as this question is asked, one begins to think like a mathematician should. Let's try and work it out, like a mathematician would. For instance, consider the calculation

6÷3/4

Conceptually, there are many things that build up to being able to really understand why the answer to this calculation is 8. You certainly need to have some visual representation of division and of course, you need to be able to count.

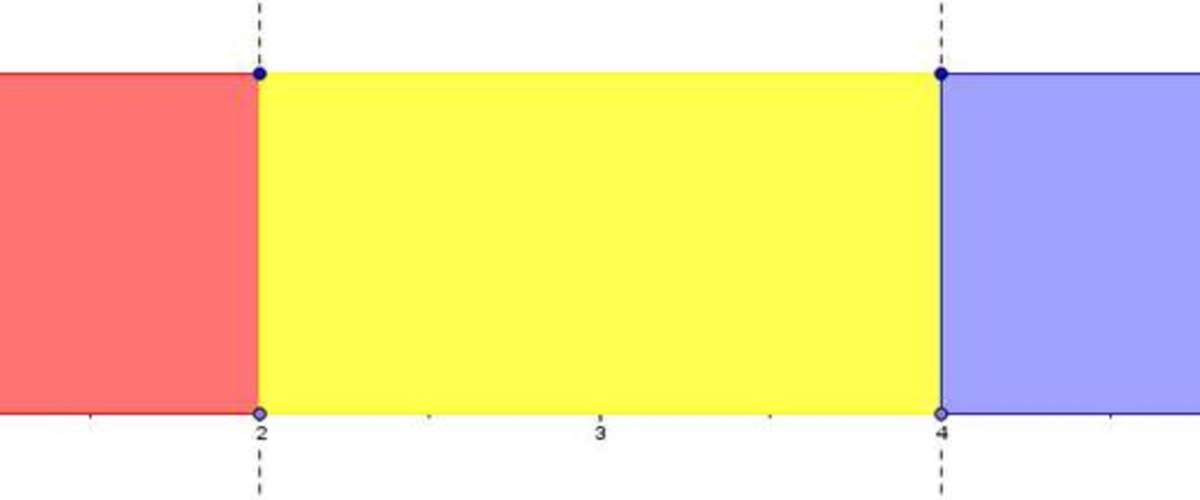
Let's first of all reconsider the following problem; 6÷2. Now, division is essentially an act whereby we break, in this case, the six 'wholes' into a collection of two 'wholes' (how many twos are there in six?), something like this:

...where each 'block' is worth exactly two. Clearly, the answer here is three. I know what you are thinking, "I already knew that". Of course you did, but it is so useful! Suppose instead I decided to break up the six wholes into ¾  blocks instead, or the six wholes into ¼ blocks - actually, let's go one step further and just consider how many times a ¼ fits inside one whole:

We immediately see that exactly four quarters fit into one whole. If I repeated this six times, surely I would have 24 quarters in total? Yes, you must! Count them! Even better, this shows that

6÷ 1/4 = 24

But, of course, that is not the final story - we want to know how many ¾ fit into six. All we now need to do is group our ¼ into groups of ¾.  The final picture is

Now, see how I have taken the 6 wholes given, broken it all up into quarters (dotted lines) and then grouped these quarters into groups of three! I can count exactly 8 full groups of ¾ in six, hence the solution is 8.

So, what can we conclude? How can we generalise?

Well, when dividing by a fraction, we first think about breaking one whole into equal blocks of the denominator (number on the bottom) of a fraction: in this case the denominator was 4, so we broke one whole into four one-quarters, of which there are four in one whole so there must be 6 x 4 = 24 quarters that can be placed into six wholes. But we are not done, we then collected together each of our ¼ into groups of three. In the six wholes, there are now three times too many blocks of 1/4, so we must divide the total number of one-quarters by three to make it groups of three! Hence,

6 ÷3/4=(6×4)÷3=24 ÷3=8,

is a mathematical statement showing what I actually did, using numbers instead of words. At the beginning of this post I mentioned, "take the second fraction, flip-it, and then multiply", which is fine:

6 ÷3/4=6×4÷3=6×4/3=(6×4)/3=24/3=8.

It is, however, far more interesting to take a mathematician's view - use what you know to find something new; explicitly, a quick way to divide any number (or fraction) by a fraction, implicitly, the observation that dividing by a number does not necessarily mean that the number gets smaller...